昨天帶到了線性迴歸的函數，讓我們再來看一遍，

觀察值 = f(x) + noise

這裡的 f(x) 是我們想要找到的理想函數，但現實沒有我們想的這麼容易，我們用雜訊(noise)來模擬。

假設 理想函數是

f(x) = 3.8*x + 8.7

用 Python 來模擬就是

x = np.linspace(0, 1, 50)
y = 3.8*x + 8.7 + 0.2*np.random.randn(50)

接下來，個別來看看：
首先 np.linspace(0, 1, 50) 是什麼意思呢?
不知道，就讓 colab 幫我們 output 出來吧~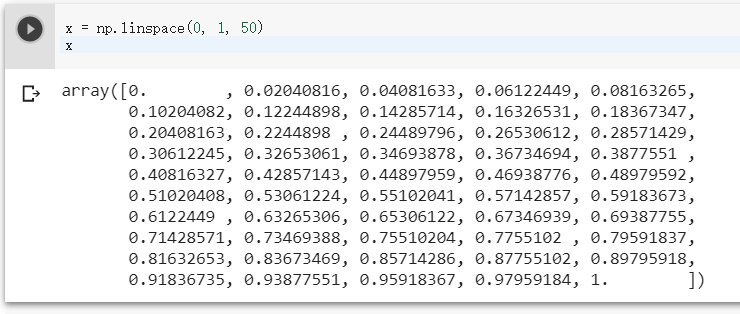

沒錯! 直接打上變數x，他就會output我們想知道的結果！
所以 np.linspace(0,1,50)的意思就是 幫我產生 0 ~ 1 之間(包含)的點。

再來看 y ，np.random.randn(50) 從字面上看 會產生亂數，再給他跑跑看output出來。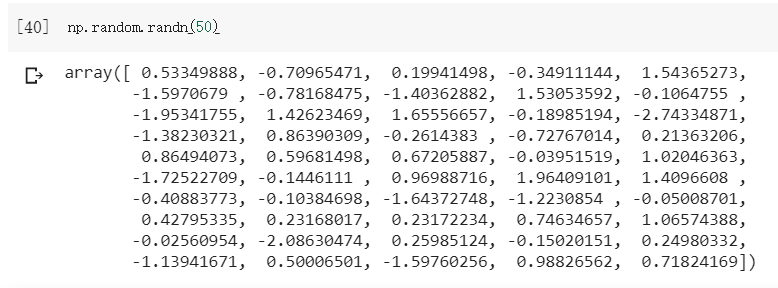

產生了50個亂數呢!

假如我們先以亂數來跑看看

x = np.linspace(0, 1, 50)
y = np.random.randn(50)
plt.scatter(x,y)

第一次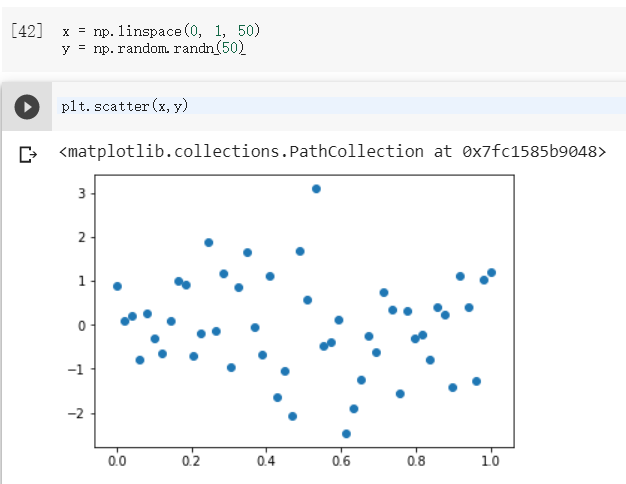

第二次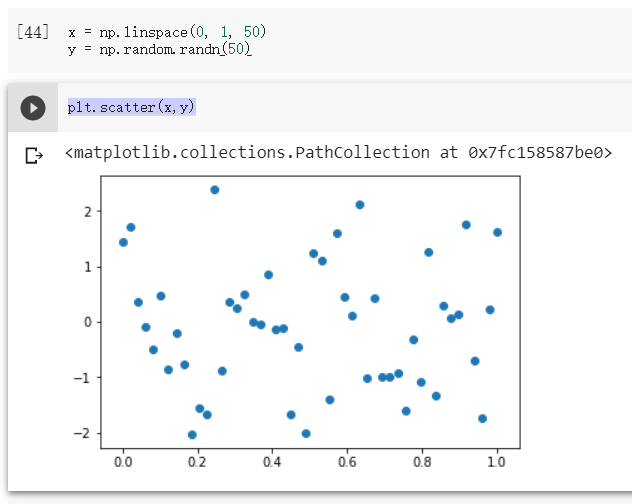

第三次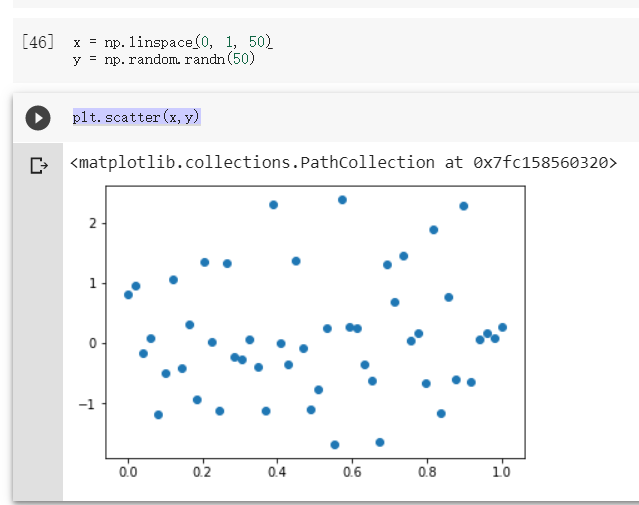

可以發現 亂數的 range 主要落在 0 正負1~2 ，

再來看看一般的線性函數會畫出甚麼，

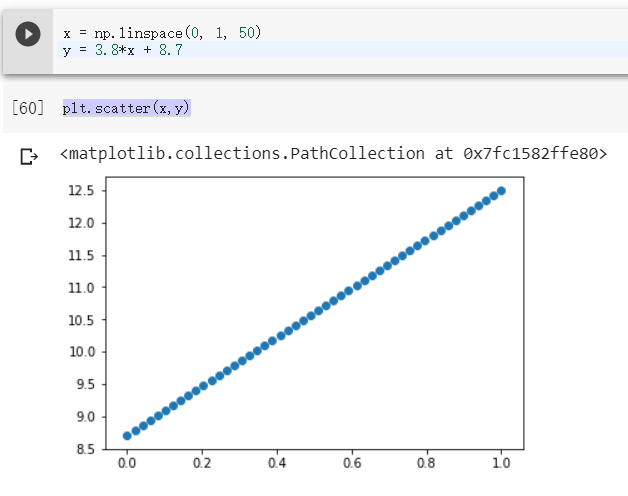
想當然爾，就是看似直直的直線...點的數量再多就會連成線囉!

x = np.linspace(0, 1, 50)
y = 3.8*x + 8.7 + np.random.randn(50)
plt.scatter(x,y)

加上我們的亂數變量(noise)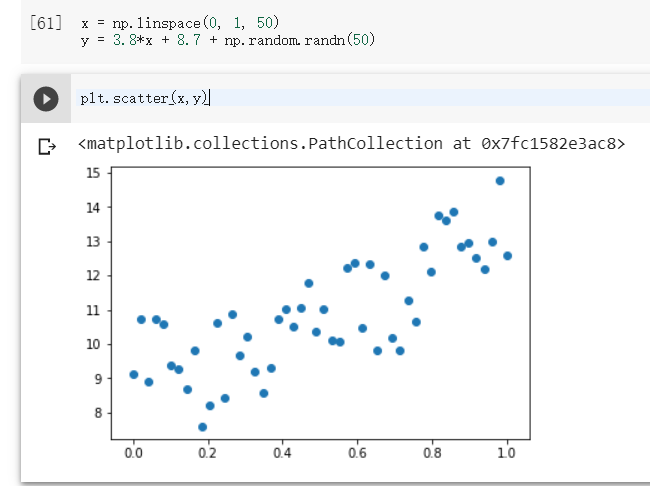

至於 noise 前面的乘數，決定 noise 的程度，
當乘數為 0.2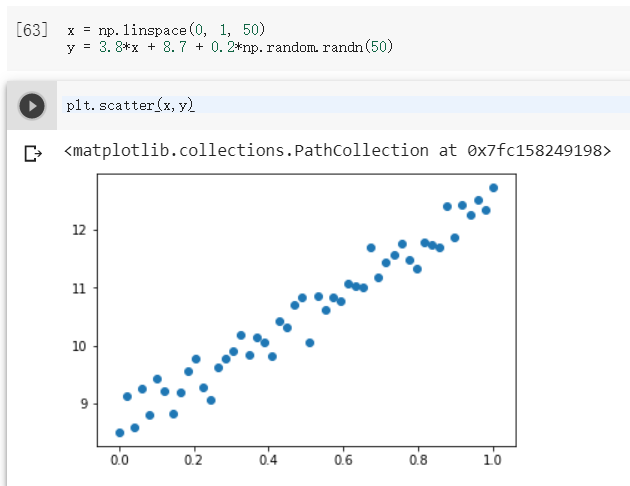

當乘數為 0.8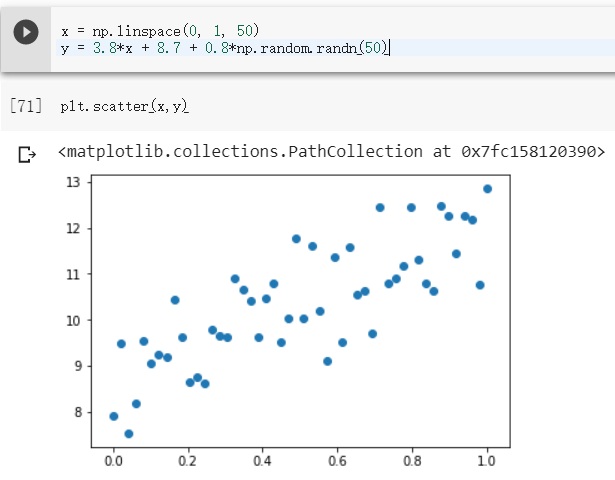

可以發現 乘數接近 0，點就越接近線性函數的直線
越接近1，點就越分散。